… for Visual Effects

Tip #654: What is a B-spline curve?

Larry Jordan – LarryJordan.com

The key benefit of B-spline curves is their smoothness.

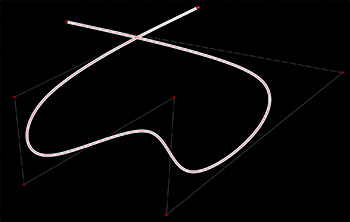
A B-spline function is a combination of flexible bands that passes through the number of points that are called control points and creates smooth curves. These functions enable the creation and management of complex shapes and surfaces using a number of points. (That’s what it says here, not that I fully understand it.)

The term “B-spline” was coined by Isaac Jacob Schoenberg and is short for basis spline. B-splines are more general curves than Bezier curves. More simply, a Bezier is a special case of a B-spline.

The big difference between B-splnes and Bezier curves is smoothness. B-splines are made out several curve segments that are joined “smoothly.” Bezier’s on the other hand, can have corners.

A B-Spline curve can be a Bezier curve whenever the programmer so desires. Further B-Spline curves offer more control and flexibility than a Bezier curve. It is possible to use lower degree curves and still maintain a large number of control points. B-Spline, despite being more useful, are still polynomial curves and cannot represent simple curves like circles and ellipses. For these shapes, a further generalization of B-Spline curves, known as NURBS, is used.

EXTRA CREDIT

I’d share the math of B-splines with you, but, frankly, I don’t understand it. A Google search will turn up lots of university references.